基础
1…Python的可变数据类型和不可变数据类型?
Python 中的可变数据类型有列表、字典和集合;不可变数据类型有整数、浮点数、字符串、元组和布尔值。
可变对象可以在原来地址上修改元素,不可变则不行(即不能在自己身上增删改),若要修改可以使用对象拼接赋值给新的对象,总之不能修改自身
2.Python的内置数据结构?
列表,集合,元组,字典
list:有序可修改。通过索引进行查找、切片。使用方括号[ ]表示;
tuple:有序不可修改。可查询、切片操作。元组将多样的对象集合到一起,通过索引进行查找。用小括号( )表示;
set:集合,无序可修改,无重复,无索引,不能跟列表一样切片。自动去重。使用set([ ])表示;
dict:字典是一组key-value,通过key查找,无顺序,用{ }表示。
3.字符串逆序
1 | s[::-1] |
4.数值
没有最大整数def
1 | float('inf') |
5 .列表
lines=sorted(lines)words.reverse()原地翻转ls.append(path[:]):保存列表结果用这个。ls.append(path),ls.pop(0)ls.sort()原地排序
对这种二维列表去重
[[1, 2, 5], [1, 7], [1, 6, 1], [2, 6], [2, 1, 5], [7, 1]]
由于列表是不可哈希的类型,需要先将每个子列表转换为元组,再使用集合进行去重,最后再转换回列表。
为元组是可哈希的,可以作为集合的元素。然后,我们将这些元组放入集合中,集合会自动去重。
extend(iterable): 将可迭代对象中的元素添加到列表的末尾。
6.del 删除
在这个例子中,我们首先创建了一个列表[1, 2, 3]并让变量a指向它。然后,我们让变量b也指向这个列表。当我们使用del a时,我们只是删除了变量a,而列表[1, 2, 3]仍然存在,因为变量b仍然指向它。
所以,当我们说*“删除的是变量而不是数据*”时,我们的意思是del关键字删除的是变量(也就是数据的引用),而不是实际的数据对象。希望这个解释对你有所帮助!
1 | a = [1, 2, 3] |
1 | a = [0, 2, 2, 3] |
7.字符串方法
1 | s.strip() |
8.if not, 真假
False、None、空字符串""、数字0、空列表[\]、空字典{}或空元组()
if not stack: 当stack为NOne
9.is和== 的区别
is判断两个对象的内存地址是否相同 == 判断两个对象的值是否相同
10.字典
字典的键必须是不可变的类型。不可以使用列表作为键。字典键的常见类型包括整数、浮点数、字符串、元组等不可变类型。
1 | # 字典的键可以是整数 |
如何根据key进行排序?
在 sorted() 函数中指定要排序的元组列表和一个 key 参数,该参数用于指定排序的关键字。在这里,我们可以将 key 参数设置为 lambda x: x[0],以根据元组的第一个元素(即键)进行排序。
1 | my_dict = {'apple': 10, 'orange': 5, 'banana': 20, 'grape': 7} |
lambda函数可以换:
1 | def get_key(item): |
方法
get(k,default)
11.推导
可以从一个数据序列构建另一个新的数据序列的结构体
1 | names = ['Bob','Tom','alice','Jerry','Wendy','Smith'] |
12.常用的模块,标准库
1 | import logging |
13.迭代器
迭代器是一个可以记住遍历位置的对象。
迭代器有两个基本的方法:iter() 和 next()。
许多内置对象都是可迭代的,例如列表、元组、字符串等。
1 | class MyIterator: |
14. map(),filter(),reduce()
1 | length=list(map(lambda x:len(x),names)) |
15.遍历技巧
1 | for k in {'a':1,'b':2} : |
字典中遍历时,关键字和对应的值可以使用 items() 方法同时解读出来:
1 | knights = {'gallahad': 'the pure', 'robin': 'the brave'} |
序列中遍历时,索引位置和对应值可以使用 enumerate() 函数同时得到:
1 | for i,v in enumerate(names): |
同时遍历两个或更多的序列,可以使用 zip() 组合:
1 | questions = ['name', 'quest', 'favorite color'] |
要按顺序遍历一个序列,使用 sorted() 函数返回一个已排序的序列,并不修改原值:
1 | for f in sorted(set(names)): |
16.输入输出
读写文件
1 | f=open('temp.txt','w') |
pickle 模块:基本的数据序列和反序列化。
1 | import pickle |
17.嵌套函数,外部变量
1 | def outer_function(): |
好避免在函数之间共享状态,而是通过函数参数和返回值来传递信息
但是res[] 列表可以
18.copy 拷贝:
深拷贝(deep copy)和浅拷贝(shallow copy)是两种不同的复制方式,它们主要针对复杂对象(例如嵌套的列表或字典)中的子对象的复制方式而言。
- 浅拷贝:只是复制了容器对象本身和对其元素(复杂对象)的引用。 即新对象修改元素会改变原始元素
res.append(path.copy())和res.append(path[:])都用于向列表res中添加列表path的副本。
path.copy():创建列表的浅拷贝,会复制列表中的元素。如果元素是对象如列表,则不会复制对象本身内容。- 实际上,对于包含整数、字符串这种的列表,
copy和[:]效果一样,
- 深拷贝:创建一个对象,递归复制对象内所有元素,是完全独立的副本
path.deepcopy()实现深拷贝
19.转换
bin
20.集合
1 | s.add(x) |
21.循环
1 | for i in range(6): |
20.生成器
生成器(Generator)是一种特殊的迭代器,它允许按需生成值,
生成器使用 yield 关键字来实现暂停和恢复执行,允许函数在每次产生值后暂停并在下一次调用时继续执行。
定义生成器:
- 生成器函数:使用
yield关键字的函数。
1 | def my_generator(): |
- ** 生成器表达式** : 类似于列表推导式,但使用圆括号。
1 | gen = (x for x in range(1, 4)) |
yield和return:
相同点:都是返回程序的执行结果;
区别:yield返回结果但程序还没有结束,return返回结果表示程序已经结束执行
22.谈谈对不定⻓参数的理解?
在不确定需要传多少参数时使用,args表示位置参数,元组形式保存,kwargs表示关键字参数
1 | def cache(func): |
23.多线程 threading 模块
- 方法:
threading.Thread(target=modify_shared_resource):创建线程,指定启动执行函数
run(): 用以表示线程活动的方法。
start():启动线程活动。
join([time]): 等待至线程中止。这阻塞调用线程直至线程的join() 方法被调用中止-正常退出或者抛出未处理的异常-或者是可选的超时发生。
isAlive(): 返回线程是否活动的。
getName(): 返回线程名。
setName(): 设置线程名
threading.Lock()
threading.Semaphore(value=2)
threading.Event() - 案例:
1 | import threading |
- 线程同步
(1) 互斥量
1 | import threading |
(2)信号量
1 | import threading |
(3) 事件(Event):
事件用于线程之间的通信,一个线程可以等待事件的触发,而另一个线程可以触发事件。
1 | import threading |
(4).条件变量
(5).队列
24.with
with 语句是 Python 中用于简化资源管理的语法结构,通常用于对文件、网络连接、线程锁等资源进行管理。
25。collections
26. 面向对象
接口:
1 | from abc import ABC, abstractmethod |
数据结构和算法
1.二叉树、
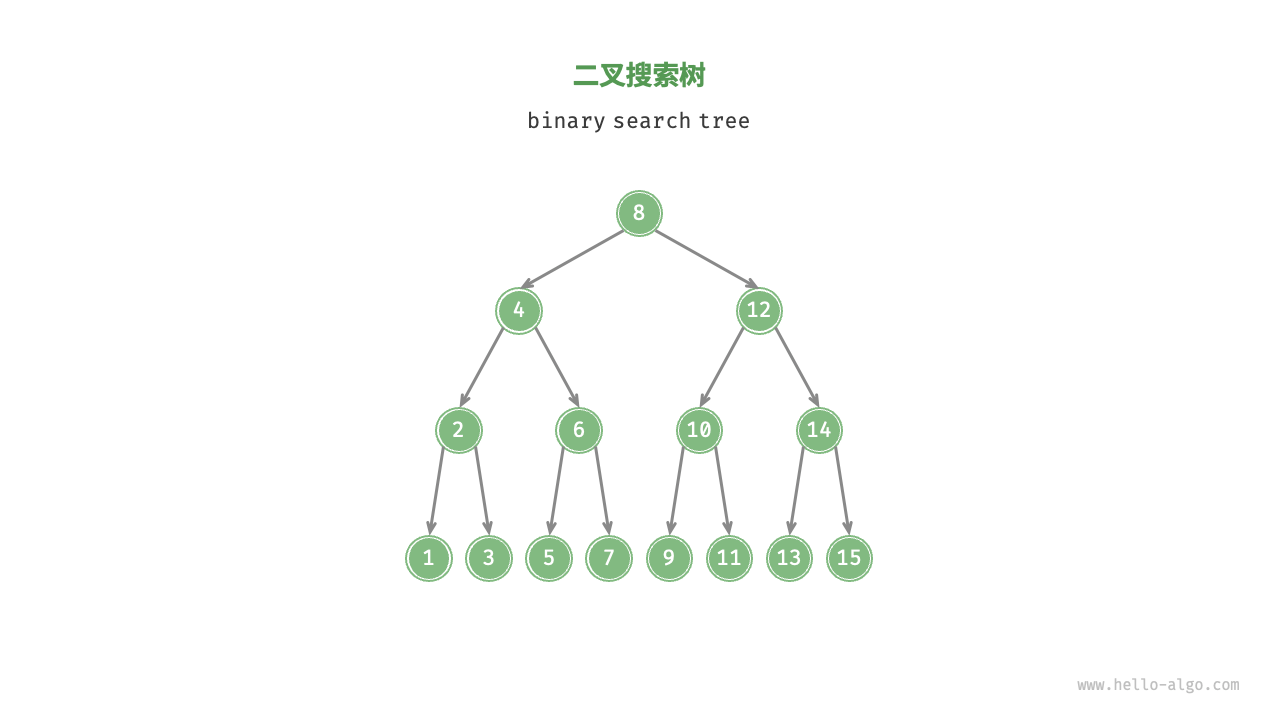
1.1二叉搜索树
- 对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
- 任意节点的左、右子树也是二叉搜索树,即同样满足条件
1. - 中序遍历是一个升序序列
1.2 完全二叉树
除最底层最右边的节点没充满
- 最后一个非叶子节点
- parent=(i-1)//2
- 通过高度 计算结点个数
- 左子树高度>右子树高度:右子树是满二叉
- 左子树高度=右子树高度:左子树是满二叉
1.3 平衡二叉树
左右两个子树的高度差的绝对值不超过 1 。
1.4 遍历
-
深度优先搜索(DFS):在DFS中,从起始节点开始,沿着一条路径尽可能深入直到到达叶子节点,然后回溯到前一个节点,继续探索其他路径。这一过程以递归或栈的形式实现。
前序和后序都是DFS -
广度优先搜索
从右到左层序遍历 -
已知中序和后序遍历,如何确定这个二叉树?
1 | # 使用深度优先搜索(DFS)计算每一层节点的平均值时,需要额外记录每层的节点值和节点数量。 |
1.5 路径
- 因为列表是可变对象,如果直接将
path添加到res,后续对path的修改会影响已经添加到res中的路径。 - 使用
path.copy()创建路径的副本,确保不同路径之间的独立性。
1 | # 回溯方法:所有路径 |
1 | # 检查路劲和 |
2.回溯法
简单来说,回溯算法采用了一种 「走不通就回退」 的算法思想。
回溯算法通常用简单的递归方法来实现,在进行回溯过程中更可能会出现两种情况:
- 找到一个可能存在的正确答案;
- 在尝试了所有可能的分布方法之后宣布该问题没有答案
全排列
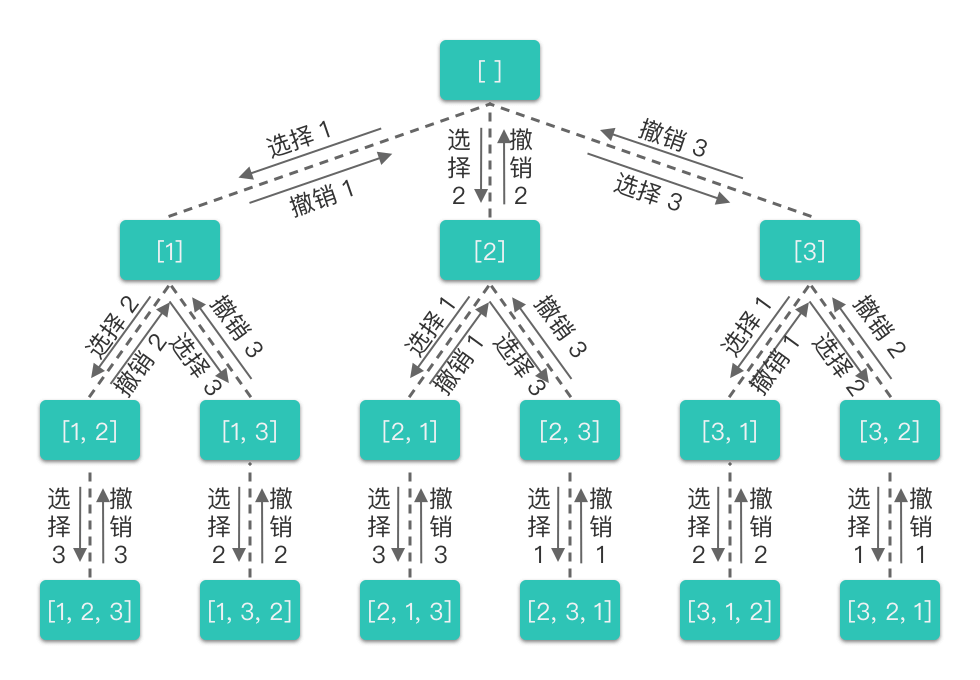
模板:
1 | res = [] # 存放所欲符合条件结果的集合 |
子集:
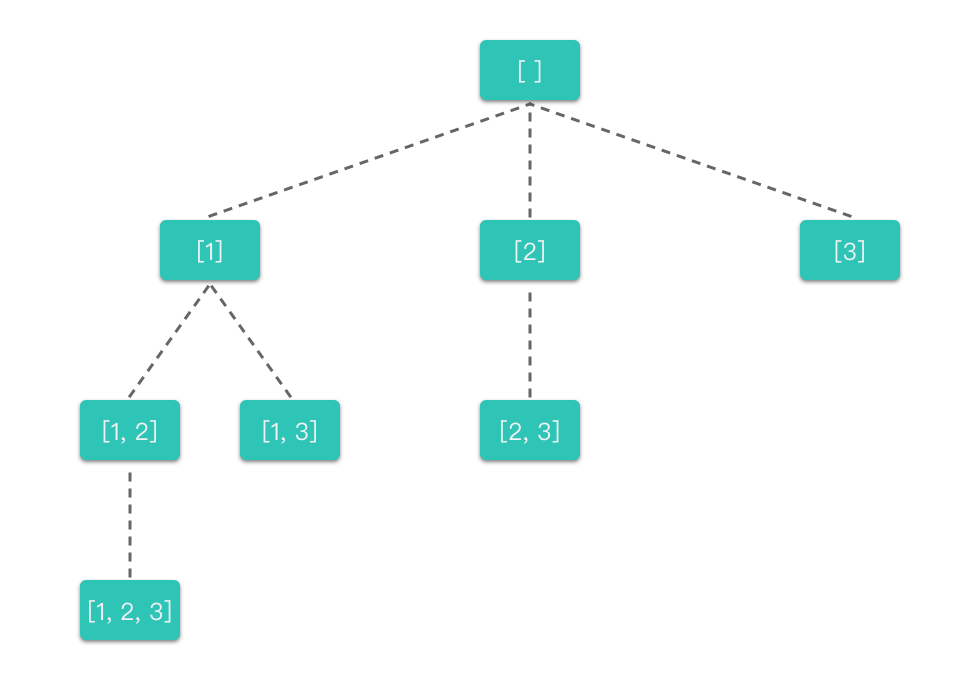
backtracking(nums, index):函数代表的含义是:在选择nums[index]的情况下,递归选择剩下的元素。
剪枝
3.栈
3.1最小栈
:能在常数时间内检索到最小元素的栈。
使用一个 min 变量记录当前栈中的最小值确实是一种方法。然而,当元素被弹出时,如果弹出的正好是最小值,那么我们就需要重新遍历整个栈找到新的最小值。这样在 pop 操作的时候就会变得更加耗时。
1 | class MinStack: |
3.2单调栈:
单调递增栈:
- 栈底到栈顶递增。
- 新元素入栈,要保持递增,需要弹出所有比他大的元素
- 可以快速找到它前面比它小的元素和后面比它小的元素。
- 求解某个元素的下一个更大元素(Next Greater Element): 在一个数组中,找到每个元素右边第一个比它大的元素。
例子:每日温度
1 | 输入: temperatures = [73,74,75,71,69,72,76,73] |
找到每个元素下一个比他大的元素, 单调递减栈。
*stack*=[0(73)],*stack*=[2(75),3(71),4(69)]这种写法 好理解
模板
1 | for i in nums: |

4.递归和迭代
递归,函数调用,栈帧:
参数压栈, 接受返回值,
就类似栈帧, 把调用参数逐个压栈,
多个参数可视为一个元组压栈.
1 | def maxDepth(self, root: Optional[TreeNode]) -> int: |
5.贪心算法
贪心算法基于当前情况,做出下一步的最优解。因此,总是逐步迭代,问题规模逐渐变小。贪心算法每次局部最优,但不一定达到全局最优。需要证明达到,或者达到近似。
6.指针
快慢指针:
如果存在循环,终会相遇。
双指针:
明确含义
一般用while语句
滑动窗口
7.动态规划
7.1 五部曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化:根据递推公式得到需要初始化的底层值
- 确定遍历顺序:不同遍历顺序?
- 举例推导dp数组:验证结果思路,然后才写代码
除了写循环,也可以写成递归
双层dp:
某一点的状态需要遍历,使用其他节点内容填充,
即:
1 | for ele in list: |
7.2案例
子集划分
给你一个 只包含正整数 的 非空 数组
nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
问题:是否存在一个子集的和为 nums和的一半?
dp[i][j]:前i个元素中是否存在一个子集和为j
dp[n][nums和/2]:最终结果
dp[i][0]:子集包含空集,和为0
状态转移:dp[i-1][(j)]
如果前i-1个元素存在子集和为j,那么前i个元素就存在子集和为j。 i元素不放入子集。
如果前i-1个元素存在子集和为j-nums[i],那么前i个元素也存在子集和为j。 i元素放入子集
如果前i-1个元素不存在子集和为j,且和不为j-nums[i],那么前i个元素也不存在和为j。
~~方法一:
dp[i][j]:前 i 个石头中选择若干个,使得它们的总重量不超过 j 时,可能的最大石头重量。
dp[n][sum//2]: 前n个元素,选择若干个,在其和不超过sum//2情况下,的最大和
结果:sum-dp[n][sum//2]-dp[n][sum//2]
1 | dp[i][j]=max(dp[i-1][j],dp[i-1][j-stone]+stone) |
方法二:
dp[i]:是否存在一些石头,重量和为i。
结果:找到最后一个true,即为最大重量
1 | def lastStoneWeightII(stones): |
方法三:
dp[i]:总重不超过i的情况下,最大重量
1 | dp[j] = max(dp[j], dp[j - stone] + stone) |
不同的二叉搜索树: [1…n]构成的…个数
卡特兰数:
判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
!()[https://raw.githubusercontent.com/ddongzi/ddongzi.github.io/main/image/markdown/20231220161833.png]
回文子串:
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
dp定义:
dp[i]: s[i,j]是否存在回文子串。布尔类型
状态转移(递归):
dp[i][j]= s[i]==s[j] and dp[i+1][j-1]
特殊值处理,分情况:
i==j : True
j-i>=1:True
返回值:
用res 计数
初始化:
dp[i][j]:False
遍历顺序:
![[Pasted image 20231220175747.png]]
1 | for i in range(n-1,-1,-1): |
换零钱
dp[i]: 凑成i 元地最小硬币书
8.背包问题
背包问题是动态规划
8.1 01背包
问题描述:
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
例子:背包最大重量为4。
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
| 二维dp数组01背包: | ||
| 1. dp数组定义,下标定义: | ||
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。 |
||
| 表示前i个物品,放进j容量背包地价值最大总和。 | ||
| ![[Pasted image 20231226231423.png]] |
- 递推方式
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3. 初始化
dp[i][0]=0初始化
![[Pasted image 20231226231731.png]]
dp[0][j]初始化
![[Pasted image 20231226232510.png]]
其余值初始化:
由递推公式知道,是由上一层推导出来的,递推方向向右下,所以其余初始值都被覆盖,设置0即可
![[Pasted image 20231226232948.png]]
- 确定遍历顺序
遍历顺序不影响公式推导,所需的数据都是固定左上角唯一的
![[Pasted image 20231226233928.png]] - 举例推导dp数组
做动态规划的题目,最好的过程就是自己在纸上举一个例子把对应的dp数组的数值推导一下,然后在动手写代码!
![[Pasted image 20231226234414.png]]
代码:
1 | limit=4 |
一维dp数组(滚动数组)
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。
这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
本质是一层一层计算。
![[Pasted image 20231226232510.png]]
- dp数组定义:
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。 - 递推公式:
1 | dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); |
- 初始化:
初始化为0, 右边通过左边地推而来 - 确定遍历顺序
1 | for(int i = 0; i < weight.size(); i++) { // 遍历物品 |
如果背包容量是正序遍历,显然dp[2]中物品0被重复放了2次,不符合只放一次的背包。
1 | dp[1] = dp[1 - weight[0]] + value[0] = 15 |
如果背包容量是倒序遍历,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
1 | dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0) |
此外,不可以颠倒内外部循环。
5. 举例推导dp数组
![[Pasted image 20231227114952.png]]
8.2 完全背包:
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
01背包和完全背包唯一不同就是体现在遍历顺序上
8.分治:
拆解问题,尤其是常规加上额外条件时
9.数组
元素是删除不了的,只能覆盖
滑动窗口
双指针
10.堆
堆是一种特殊的数据结构,它是一个完全二叉树,且父节点的值小于或等于其子节点的值。
heapq 是 Python 标准库中的一个模块,提供了一个实现堆队列算法的模块。堆是一种特殊的数据结构,它是一个完全二叉树,且父节点的值小于或等于其子节点的值。在 Python 的 heapq 模块中,堆总是以列表的形式表示,且堆的第一个元素是最小(或最大)的元素。
heapq 提供了一些用于在堆上进行操作的函数,包括将列表转换为堆、向堆中插入元素、从堆中弹出最小(或最大)元素等操作。其中,最小堆可以用于解决一些优先级队列的问题,而最大堆则相反。
1 | import heapq |
大根堆:
将元素的值取相反数插入堆 max_heap = [-x for x in max_heap]
堆是一种数据结构,具有以下主要特点:
-
有序性:
- 堆是一个特殊的树形数据结构,通常是一个完全二叉树。
- 堆中的每个节点都有一个键值,且具有堆属性,即对于每个节点
i,其父节点的键值要么小于等于i的键值(最大堆),要么大于等于i的键值(最小堆)。
-
堆的种类:
- 最大堆: 每个节点的值都大于或等于其子节点的值,根节点是最大的。
- 最小堆: 每个节点的值都小于或等于其子节点的值,根节点是最小的。
-
堆的表示:
- 堆通常使用数组来表示。在数组中,如果节点
i存储了一个元素,则其左子节点为(2*i + 1),右子节点为(2*i + 2),父节点为((i-1)//2)。
- 堆通常使用数组来表示。在数组中,如果节点
-
插入和删除操作的复杂度:
- 插入和删除堆中的元素的时间复杂度通常为 O(log n),其中 n 是堆中元素的数量。
- 插入操作:将新元素插入到堆的末尾,然后通过一系列交换操作维持堆属性。
- 删除操作:删除堆的根节点,将堆的最后一个元素移到根位置,然后通过一系列交换操作维持堆属性。
-
堆的应用:
- 堆常用于优先队列的实现,其中最小堆可以用于实现最小优先队列,而最大堆可以用于实现最大优先队列。
- 堆排序算法使用最大堆或最小堆来进行排序。
- 堆还可以用于实现一些高效的算法,如Dijkstra算法和Prim算法。
总体而言,堆是一种非常有效的数据结构,特别适用于需要快速查找最大或最小元素的场景。
11.排序算法
1 | #每次选择最小的元素,放在已排序的部分的末尾。 |
12.广度优先和深度优先搜索
BFS和DFS 都是图搜索算法。
二叉树是特殊的图结构。
深度优先:
特点:认准一个方向搜索,直到碰壁后(到达终点后)再换方向。换方向是撤销原路径,改为下一个节点。 换方向过程就是回溯。 使用栈(或者递归调用)维护访问的节点。
场景:找到一条路径,或者找到所有路径
代码框架:(实际就是回溯)
1 | dfs(参数) { |
广度优先-:
特点:从起点出发,以起始点为中心一圈一圈进行搜。搜索到终点即为最短路径。 搜索方向为四周
场景:寻找最短路径, 使用队列来维护节点, 常使用visited[]标记
![[Pasted image 20231226170753.png]]
![[Pasted image 20231226170825.png]]
代码框架:
使用队列实现
1 | from collections import deque # 双端队列 |
- 深度优先
1 | def numIslands(self, grid: List[List[str]]) -> int: |
- 广度优先
![[Pasted image 20231226175011.png]]
1 | def numIslands(self, grid: List[List[str]]) -> int: |
面试题
2.什么是堆?什么是栈?栈和堆的区别是什么?
数据结构:
堆:是一种无序的数据结构,可以看成完全二叉树。
栈:后进先出的数据结构,系统内存:
堆 :没有特定的操作顺序,一般用于动态分配内存空间。
栈:一般用于存储局部变量、函数调用以及程序执行过程中的临时数据。
最大区别在于它们的内存分配方式不同,栈由系统自动分配和释放,而堆的分配和释放需要程序员手动控制。
3.简述数组,链表,队列,堆栈的区别?
数组、链表、队列和堆栈都是常见的数据结构,它们在存储和操作数据上有不同的特点。
- 数组(Array):
- 存储方式: 连续的内存块,通过索引直接访问元素。
- 插入和删除: 插入和删除元素可能需要移动其他元素。
- 适用场景: 适用于元素大小已知,且需要频繁随机访问的情况。
- 链表(Linked List):
- 存储方式: 非连续的内存块,通过指针相连。
- 插入和删除: 插入和删除元素相对较快,不需要移动其他元素。
- 适用场景: 适用于元素大小不固定,需要频繁插入和删除的情况。
- 队列(Queue):
- 操作方式: 先进先出(FIFO)。
- 插入和删除: 插入(enqueue)在队尾进行,删除(dequeue)在队头进行。
- 应用场景: 适用于需要按顺序处理的任务,如广度优先搜索。
- 栈(Stack):
- 操作方式: 后进先出(LIFO)。
- 插入和删除: 插入(push)和删除(pop)都在栈顶进行。
- 应用场景: 适用于需要后进先出顺序的场景,如深度优先搜索,函数调用栈等。
总结:
- 数组适用于需要随机访问的场景,但插入和删除较为耗时。
- 链表适用于频繁插入和删除的场景,但不支持随机访问。
- 队列适用于按顺序处理的场景,先进先出。
- 栈适用于后进先出的场景,如函数调用栈。
4.面向对象的三个特性是什么?
面向对象编程(Object-Oriented Programming,OOP)有三个主要的特性,通常被称为三大特性,它们是封装(Encapsulation)、继承(Inheritance)、多态(Polymorphism)。
- 封装(Encapsulation):
- 封装是指将数据和操作数据的方法捆绑在一起的概念。
- 封装通过将数据的内部细节隐藏起来,只暴露必要的接口,使得对象的使用者无需了解对象的内部实现细节。
- 封装有助于提高代码的可维护性,降低了对象的耦合度。
- 继承(Inheritance):
- 继承是指一个类(子类)可以继承另一个类(父类)的属性和方法。
- 继承可以减少代码的重复性,提高代码的可重用性。
- 子类可以通过继承扩展或修改父类的行为,实现了代码的扩展性和灵活性。
- 多态(Polymorphism):
- 多态是指一个对象可以以多种形态存在。
- 多态允许使用一个对象的通用接口来操作不同类型的对象,提高了代码的灵活性和可扩展性。
- 多态包括编译时多态(静态多态,例如方法的重载)和运行时多态(动态多态,例如方法的重写、接口的实现)。
- 不同的子类调用相同的父类,产生不同的结果。
1 | class Animal: |
这三个特性共同组成了面向对象编程的基础,它们使得程序更易于理解、维护和扩展。这些特性使得对象能够以更模块化、可重用的方式构建,并且有助于提高代码的质量和可维护性。
5. 什么是闭包?
闭包是指在一个函数内部定义另一个函数,并且这个内部函数能够访问外部函数的变量和参数,即使外部函数已经执行完毕,这些变量和参数仍然存在于内存中,并可以被内部函数使用。闭包常常用来实现一些高阶函数的功能,例如装饰器、回调函数等。运行时动态地改变或增强函数的行为。
- 工厂函数
1 | def mutiply_by(factor): |
- #装饰器 是一种使用闭包的常见模式,它允许在不修改原始函数代码的情况下,向函数添加额外的功能。
可以用于记录日志,记录时间
1 | def my_decorator(func): |
@staticmethod 装饰器:
1 | class MyClass: |
6. 匿名函数(lambda)/函数/闭包/对象在做实参时有什么区别?
函数:当函数作为参数传递时,仅传递其功能。
匿名函数:与函数类似,只有它们的功能作为参数传递。
闭包:当闭包作为参数传递时,函数和闭包内的数据都会被传递,从而可以同时传递功能和上下文。
对象:当实例对象作为参数传递时,它的方法和属性也会被传递。
7. 什么是进程、线程、协程、多进程、多线程?有什么区别?有什么使用场景?
- 概念
进程:操作系统中进行资源分配和调度的基本单位,一个进程可以包含多个线程。每个进程都有独立的内存空间。
线程:是操作系统能够进行运算调度的最小单位。一个进程可以包含多个线程,这些线程共享进程的内存空间和系统资源,但每个线程都拥有私有的信息。
协程:一个线程可以包含多个协程,协程通常是在单个线程中运行的,但线程是由操作系统调度的,而协程则是由程序主动控制的。协程是轻量级的,在单个线程中运行,因此不存在资源竞争,死锁问题,
多线程:指一个程序中创建多个线程,这些线程共享分配给进程的内存空间,可共享资源。
多进程:是指在操作系统中创建多个独立的进程,每个进程有自己独立的内存空间和系统资源。这些进程通过进程间通信(IPC)来共享数据和协作完成任务。 - 场景
进程:适用于需要进行大量计算或者需要充分利用CPU资源的场景,如并行计算、大数据处理等(cpu密集型任务)。
线程:适用于不需要独立内存空间的场景,如Web服务器、桌面应用程序等。
协程:适用于IO密集型的应用场景,如网络爬虫、异步编程等—》同样适用于线程。
8.什么是迭代器,为什么要使用它?什么是生成器,为什么要使用它?
拥有__iter__ ,next 魔法方法的对象就是迭代器,它是一个可以记住遍历的位置的对象。
生成器是特殊的迭代器,使用yield和next函数,有生成器表达式,生成器函数,都是为了节约内存。
区别:
在处理巨大的数据集合时,建议使用生成器来节省内存。
在遍历容器对象时,使用迭代器很方便。
9.什么是线程安全?
是多个线程同时访问共享数据时,不会出现任何问题或错误的特性。这意味着在一个多线程应用程序中,当多个线程同时访问共享资源(例如变量或对象)时,它们不会干扰彼此或产生无法预测的结果。
numpy
matplotlib
1 | import matplotlib |
pandas
数据结构:
Series:带有索引的一组数据
环境
安装 Anaconda
-
从官网下载
.sh文件后,bash运行即可 -
[Optional] 区分 Ubuntu 自带 python 和 anaconda 中的 python
Ubuntu22.04 中自带 python3,为方便起见,我们可以做一定的区分。在
~/.bashrc文件最后加入以下命令:1
2
3
4alias python3="/usr/bin/python3" # 给系统自带的python起一个别名,就叫python3
export PATH="/home/jason/anaconda3/bin:$PATH" # anaconda3中的python
BASH然后 source 一下让修改发生作用:
1
2
3source ~/.bashrc
BASH这样,输入
python3时会自动替换为/usr/bin/python3,即使用系统自带的 python;而直接输入python则是用当前环境下的 python. -
[Optional] 每次打开终端时,conda 会默认自动激活 base 环境,在命令提示符前有
(base)标志。强迫症表示这太难看了,可以用以下命令禁止自动激活:1
conda config --set auto_activate_base False